15 Lookup Arrays
Even beginning programmers quickly realize that arrays make it very easy to perform the same operation(s) on each element of a homogeneous group of elements. However, what they often don’t realize is that arrays can be used in less obvious ways as well. Lookup arrays are one example.
Motivation
Highway exits used to be numbered using consecutive integers. The first (on a particular highway) was exit 1, the second was exit 2, etc. Later, highway exit numbers were changed to correspond (at least closely) to the mile marker (i.e., the number of miles since the start of the highway). So, the exit at mile marker 1 is numbered 1, the exit at mile marker 15 is numbered 15, etc. The problem then arises of how to “convert” an old exit number to a new exit number.
Review
As you know, arrays have two important characteristics. First, each element must be of the same type (i.e., the elements must be homogeneous). Second, the indexes are consecutive, non-negative int values. However, beyond that, there are no restrictions on how they can be used.
When you are first introduced to arrays, the examples all tend to involve “data processing” of some kind. For example, they involve weekly sales, annual populations, grades on exams, etc., and the indexes are just used to differentiate the elements. However, the values of the indexes can be meaningful in their own right. For example, in the current context, the indexes could represent exit numbers.
Thinking About The Problem
All that remains to think about is whether the indexes should represent the old exit numbers or the new exit numbers. Fortunately, given the nature of the old and new exit numbers, the correct representational scheme is obvious. Except for the fact that array indexes start at 0, they seem to have the same properties as the old highway numbering system. So, if there are five exits, you can use an array of length six (with indexes of 0, 1, …, 5) to hold information about each exit. In this case, the information that you want to associate with each old exit number is the new exit number, which is, itself, an int. So, you can keep the information you need in an int[] of length six.
For example, if the new exit numbers are at mile markers 1, 15, 16, 28, and 35, you can store them in the following static array named NEW_NUMBERS:
private static final int[] NEW_NUMBERS = {-1, 1, 15, 16, 28, 35};
where the first element is -1 to indicate that there is no old exit number 0. This is illustrated in Figure 15.1.
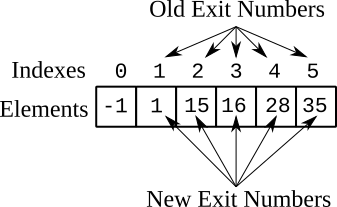
Then, the new exit number corresponding to old exit number i is just NEW_NUMBERS[i]. For example, NEW_NUMBERS[3] is the new exit number that corresponds to old exit number 3.
The Pattern
The pattern follows immediately from this example:
- Create an array in which the indexes correspond to the key that will be used to perform the look-up, and the elements correspond to the value that is to be determined.
- Create a method that validates the key and returns the appropriate element of the array for any valid key (and an error status for any invalid key).
Examples
Some other examples will help illustrate both the power and limitations of this pattern.
The Motivating Example
Continuing with the exit number example, you can implement this pattern as follows:
private static final int[] NEW_NUMBERS = {-1, 1, 15, 16, 28, 35};
public static int newExitNumberFor(int oldExitNumber) {
if ((oldExitNumber > 5)) {
return -1;
} else {
return NEW_NUMBERS[oldExitNumber];
}
}
This method returns -1 if the old exit number isn’t valid, and returns NEW_NUMBERS[oldExitNumber] otherwise.
Non-Integer Values
Of course, though the indexes must be integers (because of the nature of arrays)[1], the values needn’t be. This is easy to illustrate in an example that looks up the name of the exit that corresponds to an old exit number:
private static final String[] NAMES = {"", "Willow Ave.",
"Broad St.", "Downtown", "North End", "Lake Dr."};
public static String exitNameFor(int oldExitNumber) {
if ((oldExitNumber > 5)) {
return "";
} else {
return NAMES[oldExitNumber];
}
}
“Large” Contiguous Keys
The previous examples have keys that are contiguous and start at 0 or 1, like the indexes of an array. As a result, they are particularly well-suited to this pattern. However, it should be immediately obvious that the keys don’t have to start at 0 or 1. For example, you could use the year as a key to lookup annual data of some kind. You then need only subtract the given key from the “base” year in order to get the index.
For example, suppose you need to look up the annual sales revenues (in hundreds of thousands of dollars) for a company that was established in 2015. You need only subtract 2015 from the key in order to get the index, as follows:
private static final double[] SALES = {
107.2, 225.1, 189.9, 263.2};
public static double sales(int year) {
if ((year >= 2019)) {
return 0.0; // No sales
} else {
int index;
index = year - 2015;
return SALES[index];
}
}
Non-Contiguous Keys
Though the keys in the previous examples are contiguous, the pattern can often be used with non-contiguous but regular keys by employing the digit manipulation pattern from Chapter 3, the arithmetic on the circle pattern from Chapter 4, or the truncation pattern from Chapter 5. For example, suppose you want to be able to look-up the letter grade (either A, B, C, D, or F) for a particular numeric grade (an int in the interval [latex][0, 100][/latex]). You could implement this as follows:
private static final char[] GRADES = {
'F', 'F', 'F', 'F', 'F', 'F', 'D', 'C', 'B', 'A', 'A'};
public static char letterGrade(int numberGrade) {
int index;
index = numberGrade / 10;
return GRADES[index];
}
In this example, a grade in the 90s or 100 corresponds to an A, a grade in the 80s corresponds to a B, etc. Then, to calculate the index from the key you need only divide by 10.
If, instead, one wanted to convert from a numeric grade to either “Pass” or “Fail”, one could do the following:
private static final char[] STATUS = {'F', 'P'};
public static char passFail(double grade) { int index; index = (int) (grade / 60.0); return STATUS[index]; }
Finally, suppose you wanted to look-up the U.S. population for a particular census year. You could do the following:
private static final double[] POP = {
3.9, 5.2, 7.2, 9.6, 12.9, 17.1, 23.1, 31.4, 38.6, 49.4, 63.0, 76.2,
92.2, 106.0, 123.2, 132.2, 151.3, 179.3, 203.2, 226.5, 248.7, 281.4,
308.7};
public static double population(int year) {
int index;
if ((year >= 2020)) {
return -1.0;
} else {
index = (year - 1790) / 10;
return POP[index];
}
}
To get the index from the key in this case, you first subtract the base year (i.e., 1790, the year of the first census) from the key and then divide the result by 10 (because the census has been conducted every 10 years since the base year) to get the index.
Keys with Multiple Parts
It should be clear that, if you want to use months as the key, then you should use a 0-based index (i.e., in which 0 denotes January, 1 denotes February, etc.). It should also be clear that, if you want to use (contiguous) years as keys, then you should subtract the base year from the year of interest. Suppose, however, that you have monthly values that span multiple years. In this case, the key has multiple parts (i.e., the month and year of interest).
Fortunately, it is easy to combine several ideas to find the index of interest. In particular, you can use an expression like the following:
index = (year - BASE_YEAR) + month;
where the purpose of the different variables/constants should be obvious.
Looking Ahead
The process of turning a key of any kind into an integer (in a particular range) is known as hashing. It is one of the most important topics covered in courses on data structures and algorithms. This chapter has used some very simple and intuitive hash functions, but hash functions can be quite sophisticated, and understanding their properties can require serious thought.
- Chapter 17 on conformal arrays discusses one way to circumvent this limitation. ↵

